If you want to buy a robotic mower, it is important that you know the slope of your yard, because not every robotic mower is designed for every gradient. Here I will show you how to determine the slope of your yard.
How can the gradient or slope of the yard be determined? The gradient is usually given in percentage (%). This is the ratio of height to distance. To determine the gradient, the increase in vertical height over a horizontal distance must therefore be divided by this distance. For example, if the height difference per 100ft is 5ft, the gradient is 5/100, i.e. 5%.
In the following sections I will explain how you can precisely calculate the gradient and how to do this practically in your yard. You will also learn about the difference between percent and degree of the gradient and how to convert it. There is also a practical calculator at the end of this article.
If you are looking for suitable equipment to calculate the gradient in your yard, take a look here.
Contents
How is the gradient generally calculated?
Before you can start looking for the right robotic mower, you first need to know the maximum gradient in your yard. Whether your house is at the bottom of a hill or the top, the robotic mower will have to both climb and descend every slope in your yard, so you only need one calculation. But how is the gradient actually calculated?
The gradient is usually given as a percentage. In principle, the percentage value means that if you have a distance of X meters, you take Y% of this value, which then gives the height difference. So if you have a distance of 100ft and a gradient of 5%, that’s 100 ft x .05 = 5 ft.
Of course, this calculation is simple when you’re using 100ft as your distance, and your yard probably won’t have the same measurements. So to determine the slope (in percent) of your yard, you will need to determine the highest point and the lowest point of the slope.
You may have a rather hilly yard that has multiple slopes in it, rather than the entire yard being on one single slope. In this case, you just need to determine the gradient of the largest hill (if you have a hard time deciding which is largest, you can do this calculation for more than one slope, of course). Or, if you have what you may consider to be one large hill, but it actually has a small plateau halfway up before becoming steep again, then the slopes both above and below this flat area are considered two different slopes for the purpose of this calculation. You can either measure them separately, or if there is one which is obviously steeper, go for that one.
First, determine the lowest point of your slope. This will be your first point.

Then you determine a second point, at the highest point of the slope, and measure the distance between the two.
Rather than simply measure the ground in between, though, you have to measure the distance in a horizontal line. Think of it like a triangle: the ground distance between the first and second point make up the hypotenuse, the height difference between the first and second points is the short side of the triangle, and the third side, the horizontal distance between the two, is the longer side of the triangle. Look at the following diagram to see a visual illustration of this distance.
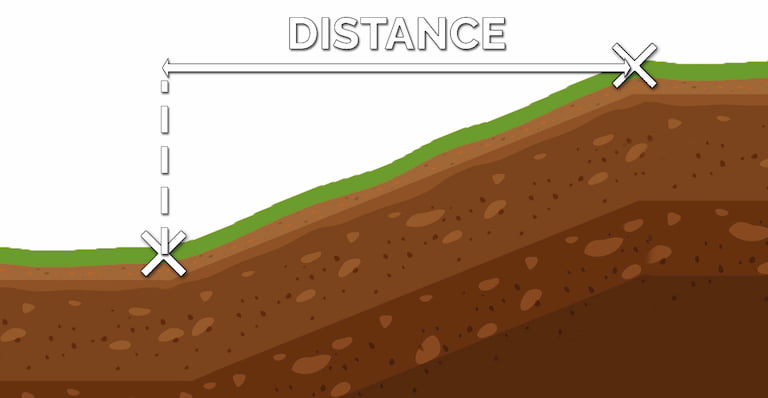
The second value you have to determine is the difference in height. If the highest point were stacked right on top of the lowest point, how many feet (or inches, or whatever you want to calculate) would be between the lowest and the highest points?

Now you have a horizontal distance between the two points and a vertical difference in height. Now you just have to divide the difference in height by the distance, then multiply the answer by 100 to get a percentage. The two values must have the same unit, so if you’ve measured one distance in feet, and the other in inches, you’ll want to convert one of the values to match the other. It is important that the units of the vertical distance and horizontal distance are the same.
Pretty simple, right? Well, in theory it is, but in real life, it can be a bit more difficult. How can you actually measure these distances and heights in your yard? With the horizontal distance you might be able to do it somehow (as I said, you have to take the horizontal distance, so it is not enough to put a tape measure over the ground). But how does it work with the difference in height? See next section.
This is how you can measure the gradient in your yard
I will now show you the cheapest method without a special measuring device to determine the gradient in the yard. You will need the following tools:
- A long straight pole
- A measuring tape
- A level
If you don’t have one of these things, you might want to check with your neighbor. In most households you will find at least one of these tools.
Now you choose the steepest place in your yard and determine a starting point and end point. These two points can be at the lowest and the highest end of the slope, as described above, to get the average slope.
If the steepness of a slope varies greatly in your yard, you should pick out the part that is steepest and determine the lower and upper points there so that you really have the maximum slope in your yard.
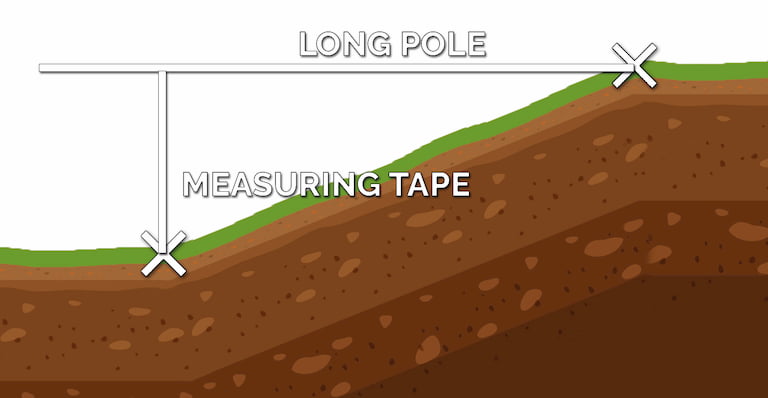
Photo: Own graphic with elements Vecteezy
Now lay one end of the rod at the upper point and lead it away in the direction of the slope, so that, except for the end at the steepest point, it is hanging in the air. The rod must be exactly horizontal. To achieve this, put the level on top and adjust the rod until the level indicates that it is horizontal.
Where the slope ends, let the tape measure hang down from the bar to the low point, pull it taut and measure the distance. The tape measure must be guided exactly vertically downwards (not at an angle). This will give you the difference in height.
From the point where you have lowered the tape measure from the rod, you now measure the distance with the tape measure along the rod to the starting point where the rod touches the ground (i.e. the top point). This will give you the horizontal distance. Of course, if you are handy with the pythagorean theorem, you can always just measure the slope itself (the hypotenuse) and use the equation a^2 + b^2 = c^2 to get the horizontal distance. However you get it is up to you.
Now all you have to do is divide the difference in height and the horizontal distance, and you have the maximum gradient in your yard in a decimal point, which you can multiply by 100 to get the percent.
Alternative measuring methods for the gradient
Instead of performing the procedure described above, you can also use other devices that make measuring much easier, but not everyone necessarily has them at home. Here I will briefly introduce some of them to you.
- Laser rangefinder: Instead of a tape measure or folding ruler, you can use a laser rangefinder. This is more practical to use and also much more accurate, but this is not necessary for our purposes. The devices usually cost $25 and upwards.
- Level with angle display: There are also levels with integrated angle display. You can simply place them directly on the slope and read the angle. If the angle is only displayed in degrees, you can convert it to percent using the method described below or the calculator at the end of this article. The cheapest models also cost about $25.
These were just a few of the many possibilities for determining the gradient in your yard. Here you will find a complete list of what I think are the best tools for determining the slope of a yard.
Gradient in percent or degrees – Difference and conversion
No matter whether on road signs or the specifications of the robotic mower, the gradient is indicated in percent with the % symbol. But sometimes you can also find a degree number with ° behind it.
It is important that you pay attention to the unit in which the gradient is given, because the percentages and the angle measure are completely different. The conversion from one value to the other isn’t a trivial matter, either. Unless you are good at calculating trigonometric functions in your head, it’s best to use a calculator to ensure accuracy.
As described above, the percentage value indicates how much the slope rises (or descends) over a certain distance, with 0% being no rise and 100% being straight up. The number of degrees is the measure of the angle and simply gives you the slope of the gradient – as if you were holding a level with angle display as described above to the gradient.
But what if you only have the angle in degrees and you want to know the percentage of it? The following formula exists for this:
Angle in percent = tan(angle in degrees) x 100
tan is the tangent, a trigonometric function. Most mid-range pocket calculators have a function to calculate it.
In the other direction, i.e. percent in degrees to angle, the formula goes like this:
angle in degrees = atan(angle in percent / 100)
atan is the arc tangent, also a trigonometric function, which is also present on pocket calculators with more than the simplest arithmetic operations. Also the calculator on most computers usually has these functions.
But so that you don’t have to dig out your pocket calculator, I have built a calculator for you, with which you can convert the two values.
Convert degree to percent
[dm name=”degrees-percent”][/dm]
By the way, you can find all the formulas for determining the gradient here: Calculate gradient
Here you also have a table with reference values:
| gradient in degrees | Slope in percent |
| 0 ° | 0 % |
| 5 ° | 9 % |
| 10 ° | 18 % |
| 15 ° | 27 % |
| 20 ° | 36 % |
| 25 ° | 47 % |
| 30 ° | 58 % |
| 35 ° | 70 % |
| 40 ° | 84 % |
| 45 ° | 100 % |
| 50 ° | 104 % |
| 55 ° | 143 % |
| 60 ° | 173 % |
Related questions
Can robotic mowers also cope with uneven terrain? Most robotic mowers can also mow on uneven lawns, as many models have quite large wheels. However, the degree of unevenness is decisive. Smaller holes and hollows up to 2 inches usually do not pose a problem, but larger hollows and depressions can become problematic.
Also interesting: Robotic mowers on a mogul slope: Can they do that?
Which robotic mowers can cope with slopes of more than 50 %? Currently (as of summer 2020) there are only a few models that can manage slopes with a gradient of 50 % or higher. These include some Ambrogio and Wiper models that can handle 50% slopes, and Husqvarna’s Automower 435x AWD and 535 AWD models that can handle 70% and even turn on slopes, which other robotic mowers cannot easily do.





